We all professionals who have gone through CA Final are very well aware of 'Options' and what methods are used for their pricing. Many have also gone through studying their formulas without knowing exactly how they all are to be interpreted and are interrelated to each other, Which pricing strategy is chosen practically by investors and What shortcuts can be used in exams. These sets of articles will be an answer to all those questions on this matter.
Let's get an overview of the basics, with an option contract, the buyer has the right, but not the obligation, to buy or sell the underlying asset or security, such as a share in Reliance. But the seller of the option, also called the "writer," has an obligation because the buyer's actions determine the seller's actions. In other words, if the buyer decides to use (or exercise) the option, the seller is obligated to satisfy the option buyer's claim; if the buyer decides not to exercise the option, it expires without any action by the seller. Now as we all know there are broadly 5 methods for calculation of Fair price of an option being
- PUT CALL Parity Theory (PCPT)
- Binomial method/Risk neutral approach and Hedge ratio Technique
- Black-Scholes Model
- Using Time value of money
Let's go through some of them and discuss them in detail
Actual meaning of PCPT
PUT CALL Parity Theory (PCPT) generally for all is a simple equation used by students and investors to find the missing figure but little do we know that it actually represents. We all know the equation of this arbitrage argument as follows:
S + PO= EP*-rt+ Co
Where
- S= Current market Price of underlying share
- PO=Option Premium of PUT option
- EP=Exercise Price
- r=Risk free rate of return
- t=Time to expiration
- Co= Option Premium of CALL option
What does it actually mean?
It represents two portfolios whose value at any point of time from t=0 till expiration date will always be equal. In simple terms these are simply two baskets of items whose price will be equal to each other no matter what happens to the price of the underlying security.
As illustrated below, in first basket there are two items i.e. a call option and an Investment in Risk-free Bond and in the second basket we have a Put option and the underlying security. The first basket is known as Fiduciary CALL and the second one as a Protective PUT, but the question one might be having is why the value of these baskets will be the always remain the same. The answer is implicit in their names. Let me explain with a help of an example, suppose we buy a share having at a price of Rs. 23 and at the same time buy its Put option currently trading at Rs. 1.41 and put these two aside. Now we also purchase a Call option at Rs. 5 and to match our portfolios invest an amount equivalent to the price at which we need to exercise the options i.e. Rs. 19.41, where EP is Rs. 20, Risk free rate of return being 3% p.a.in risk free bonds for a period of 1 year. Now let's analyze our baskets in all possible scenarios on expiry i.e. the CMP jumps above the EP let's say at Rs. 25 or it corrects itself at a price below our EP let's say Rs. 18.
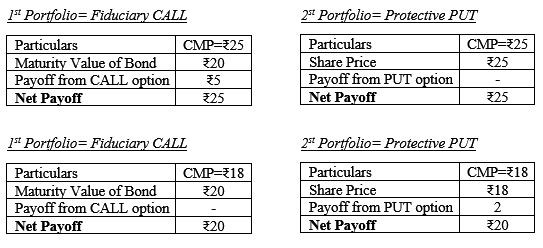
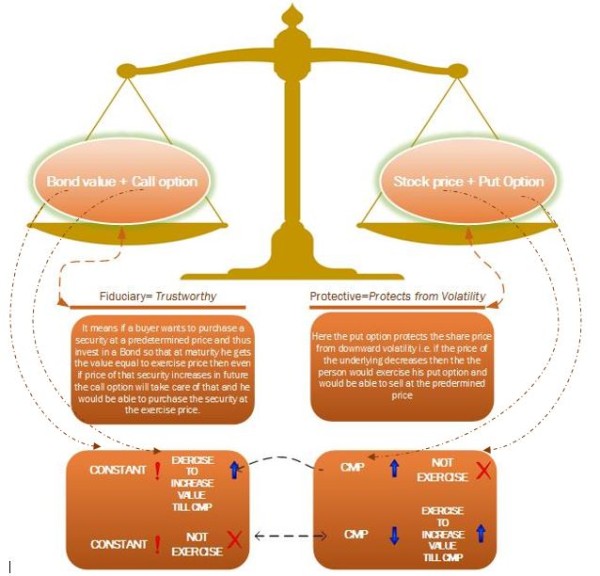
Thus the value of portfolios shall always be equal to either the stock price or the exercise price of the options of the underlying stock. It should be noted that this theory is valid only for European options and its application for American options is somewhat complicated as it is not relevant for us as in India we follow European style options.
What Practical Aspect does it have?
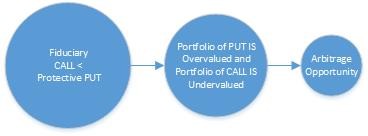
If this relationship did not hold, then one could create greater-than-riskless returns without any risk by selling the expensive combination of assets and buying the cheap combination.
Shortcut for exams and common mistakes
- Just learn the catchphrase "Sip Pepsi Be Cool" where Sip is for S, Pepsi for PO, Be for Bond value and Cool for CO.
- Some authors/teachers take a position of a call seller in the portfolios and thus subtract the call premium from the equation as S + PO - Co, please note that this is the same equation and this is another representation for calculating Total payoff and ultimately calculate the amount to be invested in Bonds so please avoid mixing the two representations and is the main equation is used take Po to be positive.
Next part is on Binomial approach and its interrelation with Hedge ratio technique.







 CAclubindia
CAclubindia