I want to know that, How the formula EOQ = Under root 2AS Divided by C is created and whats the concept is used ?
Menu
The Concept Behind EOQ ( Economic Order Quantity) ?
Replies (5)
Recent Threads
- Proprietorship to Pvt Ltd - Is Slump Sale / BTA ma
- Pan and Aadhar Link Issue
- Fund Transfer to Foreign Country and TCS provision
- ITR updated return
- Company change Status from CIRP into Active
- Can a LLP Park money in MFs and do F&O
- ACCOUNTING TREATMENT FOR FIXED ASSETS STANDING AT
- GST Rule 14A and Form GST REG-32: Simplified Regis
- Filed Hotel commission from International Company
- Reinsurance brokerage section?
Related Threads


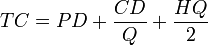 .
.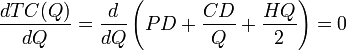 .
.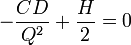 .
.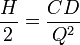
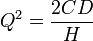
 .
.
 CAclubindia
CAclubindia