Compound interest Questions
Q1. The effective rate of interest corresponding to a normal rate 3% p.a. payable half yearly is….?
Q2. A machine is depreciated at the rate of 20% on reducing balance.The original cost of the machine was Rs.100000 and its ultimate scarp value was Rs. 30000.The effective life of machine is……..?
Q3. The population of a town increases every year by 2% of the population at the beginning of that year. The number of years by which the total increase of population be 40% is……?
Q4.The difference between C.I. and S.I. on a certain sum of money inversted for 3 years at 6% p.a. is Rs.110. The sum is….?
Q5. A machine the useful life of which is estimated to be 10 years costs Rs.10000. Rate of depreciation is 10% p.a. The scrap value at the end of its life is ….?
Q6.The effective rate of interest corresponding a nominal rate of 7% p.a. convertible quarterly is ……?
Q7. The annual birth and death rates per 1000 are 39.4 and 19.4 respectively. The number of years in which the population will be doubled assuming there is no immigration or emigration is……?
these questions are realy tough for me help guys........!!!!!!!!
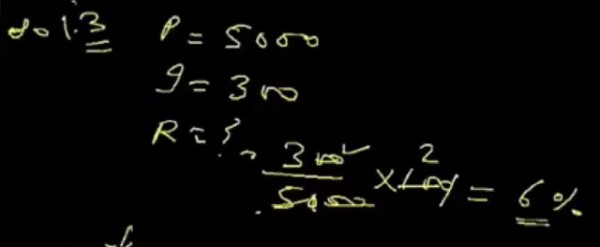



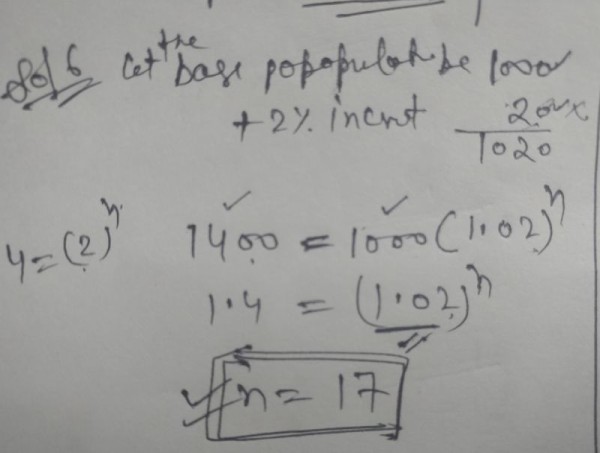
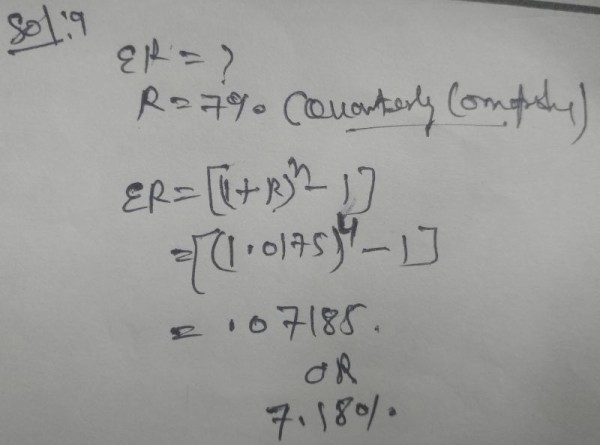
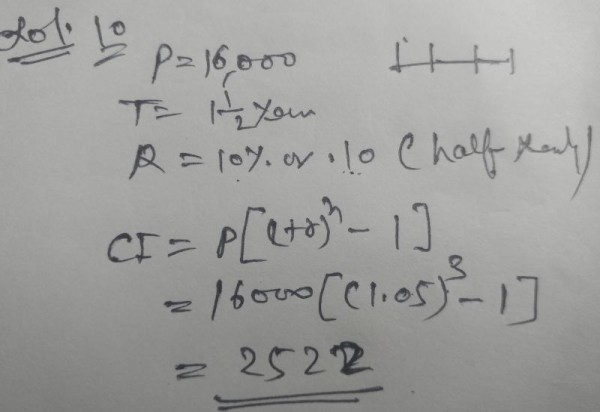


 CAclubindia
CAclubindia